CRYPTO
or MAXIMUM EFFORT
Okay. We’re gonna do a series of foundationals. Too many assumptions on my part, too much dipshittery out in the wild, way too tired of having the same five fucking arguments on different subjects.
Note that you, Dear Reader, may at various points disagree with I, Your Humble Author. This is entirely due to a failure on your part, and I, with only love, beseech you to grow and correct that.
For everyone who knows what a Diffie-Hellman exchange is, you’re not gonna find anything crazy new here, this is a foundational post, but I do try to make it fun and un-tedious. Nobody learns shit when they’re bored.
PART ONE
There are many ways to tell any parable.
A long long long time ago there was a city under siege. Some ways tell that it was the generals outside the walls who needed to to coordinate, some ways tell it was the two enemy generals trying to broker peace. The generals, regardless of version, cannot meet in person for one reason or another, as they are high value targets.
The generals must pass messages.
Due to tomfuckery, the generals know for certain that the messages will be intercepted, and likely modified or even outright forged.
This is unacceptable.
The generals resolve to solve the fucking problem.
There are certain types of math problems that are very easy to do one way, and while not impossible, very impractical to do backwards.
Allow me to demonstrate, and this is intended to be followed along with. Remember that your entire fucking mind is a muscle, and that the things you use grow stronger.
2 x 2 = ???
That’s right, 4! Very good :)
Now, what times what equals 4?
Excellent work, it is indeed 2!
This problem is relevant because 4 is the square of 2; 4 is the result of multiplying 2 by itself. 9 is another square, as it is the product of multiplying 3 by itself (3 x 3 = 9).
Some of your are genuinely irritated by this, because you’ve known this since before puberty (game recognize game), some of you are going “oh right” because you haven’t thought about shit like this in years (decades for some, bounce your grandbabies for me loves).
Some rare precious percentage of you just went “oh, i get that now”, and know that I place you above all the other groups because even still you are trying to understand, and that’s just based as all fuck in my book.
Let’s continue.
Another relevant part of the two above examples is that both 2 and 3 are prime numbers. This means that two and three are only divisible by themselves and 1. In practice, numbers like this are uncommon and they are difficult to predict.
As a practical example, try to predict the next few primes. Seriously and sincerely, avert your eyes from this page and try, the rules are actually as simple as “you can only divide the number by itself and 1”, no tricks, no gotchas.
Doot doot doot, dootin’ while ya’re tryin’ doot doot doot.
Okay, so let’s see what’s up with four. Oop, that’s the square from earlier, definitely divisible by a number aside from itself, and 1.
Five? Hm, yup, that there’s a prime number, 5 can only be divided by itself and 1.
Six? Nope, 3x2=6.
Seven? Yup! Prime!
Eight? Definitely not prime, 2x2x2=8, 2x4=8.
Nine? Nope, that’s the square of 3!
Ten? Nope, 5x2=10.
Okay, from this point forwards, you may count yourself among the certified prime number identifiers.
Identifying prime numbers is tedious, it is slow. This is also true for computers, they just do the tedious slowness faster.
This is important.
PART TWO
Encryption like what I am about to discuss was publicly discovered in the 1990s.
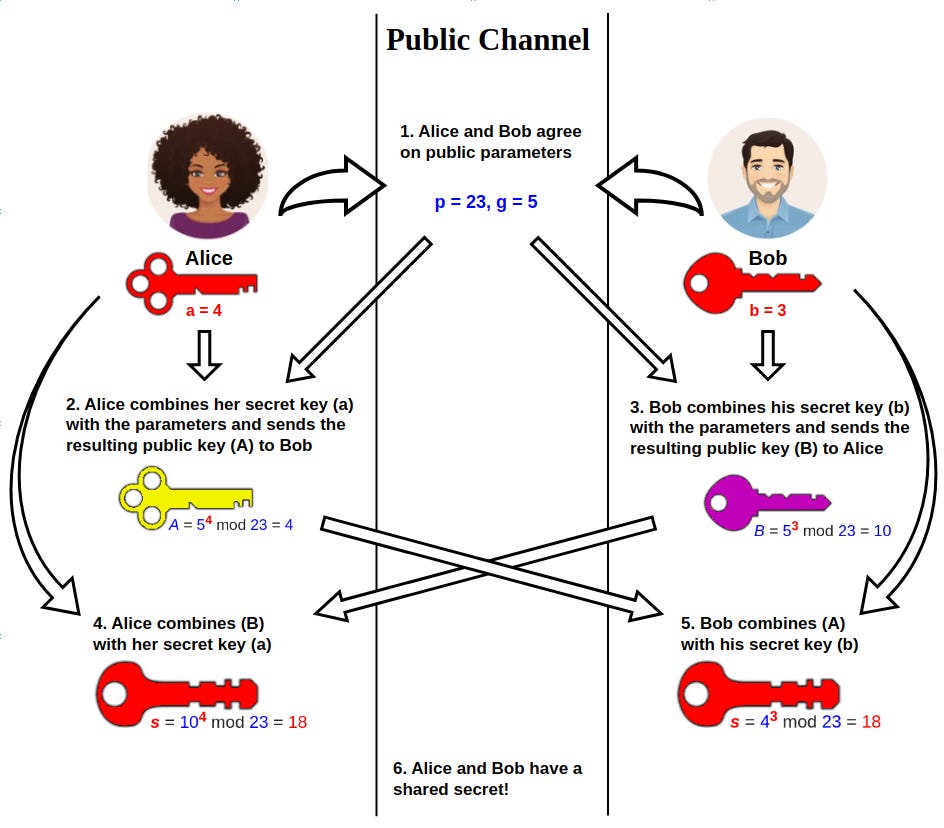
In 1976, Whitfield Diffie and Martin Hellman published a method to publicly create a shared secret between two parties. Took a few thousand years, but the generals finally found a solution.
The basics boil down to:
Two parties agree on public numbers.
Each party has their own secret number nobody else knows.
Each party does some math to the public number times their secret number, then sends it to the other party.
Because of math, by doing this the two parties arrive at the same secret number they can multiply (NOTE: THE MATH IS NOT LITERALLY MULTIPLICATION, THE GOAL IS FOR MY MOM TO UNDERSTAND THIS ESSAY, MATH, CRYPTO AND COMPUTER NERDS PLEASE STAND DOWN.) times their entire message, to get a result that appears to be gibberish to anyone without the secret number to multiply it back.
This bit right here is where a lot of people have trouble. I will elaborate, but first, here’s a picture from wikipedia that also includes the short-hand form of the math happening. Note the numbers in this picture are tiny baby number and the real secret numbers are about a full page on a standard laptop with standard font/screen sizing of base 64 encoding (binary is base 2, regular numbers are base 10, hexadecimal is base 16, the full a-zA-Z0-9 and some symbols is base 64, it lets you write REALLY big numbers with less total characters).
Thanks wikipedia.
This is a trash key I generated from the command line. (Nerds, this is a 4096 RSA SSH key since we’re eventually going to get to them bitcoins. Y’all make sure you use one of the new elliptic curves for ssh because literally everything is comped (RSA was invented by the GCHQ in the 1970s and declassified in the late 90s, check wikipedia) so you might as well get the performance boosts and keep skiddies out.
This is where we come to some math problems being hard to do backwards.
51,324,337 is the result of multiplying two prime numbers together.
Without using any form of calculator, pen and paper and your mind only, which two prime numbers did I multiply to get that result?
Pain in the ass, right? Well, by using fuckhuge numbers like the one in the screenshot above, you can actually make the problem that hard for computers too.
The full number from that above screenshot of gibberish alphanumeric text is as follows
34990577109631010069643412901766653516431959407077310801959422670042995726966522575636139762849437614122733781284935396799638887749153446030947221830622388331342299712975912921710342872235290468012966236255980197440289820357915533434219351866358628855074629990864853353368878084903036992720291446833859190548867034350340998069461819428868389882128858170079785687862418026754973814302316654880425676875992902012485055484951447780781327054125457016983991129463178134861907408459555774026198246407602169871892899190010794937605909704596989094050250529113394180930990116110821322839723139353005979659256828869335910397058367995935643516442947936268779910796624146228047040498140786530510446563644258729305229103599557927401182378377606599651979366898601052483728382891057780177134220084788158518436128277828331680733316661338565987780752766127926106039068277802362810551654234990050441466582747411648975008575283936287302148800234694607070082740243032425647898540851935367046122720925959781304854614681018090890463859839680713447513116657666178059466549830122374479584511634286043698986230742216359926754939077653976246386923128721302955488467894824145046450294740135595406522579362350729078818461843149660987013278083496685571281632830767004114494468714720841976942772713525047612423747654686629553281995599145722566201865702634330519035126744320589045623832297483039266350921060089732913259184821521189269269161438913214997410803088846287290282135077512887072949800309511025873032704183052583489185623366586094996077262409330512852066194653378652655975581438948040143756088901784525595154422471670599305602842252669948182188963813962769342829598219122799281955457071645680596574245898413516230113148605776344736934755098037835385771066833880557695344320242444248667909250958840897621812456165456404931418241945608729828931911878387621923369418067939823888227680896084494417478783901652798635861167886957927044227370317912602922445013246523808540776938747436983522991076918828822221410962155230587181050678374314725691166832138596502082613273520468553350051902951722759642229062876599349661810984525257480111329109764225788279445764103373519446495314960189313395258057088515478542343743442368230030225932557948613384154525399557874674209326407835912189961088747595501876900137652927318240952432482985275762808219008880345160529463031522799557957258781402537211690420626115281755842313768882252165566262530186021230797473324842130624737105542176411276917075882619120067255709815836342095471600112019135601406335814989520314193439375488313804029305680179166538254456288416198396987871381444133157505209284401489855476445748969717903856238374378569564291190334806374388370104437858304115131265503676384180731445894574853208857268262647728686927147115080533756512789063819128597107252956996411606924253935546848227875306779402611613229478918485822793857214125680276083612843946605056420365174080413695997219953958180733772836762683483352335923050719497408706386580038488493343796028173281266839755165207649765350158267420508663036423478480779292041251628883444782874535754473618046340565551305414167314409524365091473719980187491463267250912171955132000737411548766283074073573490793362255072631109911133077290958567745971528141924077490416801880932087879407116346694992283018641917913237773117667447811910134656955133786238409694428682302334435699848790948625254737760445164967284618079964891918086542403714022437023659588466689557815231414884332082638265830943189753920910310143473398793396995771707068488076567301451413351240062676478520716328323026822470832913112981855158035444284062713819190199263798906688435136671953048445965626095884491036413242368286381911327322087171763267294893687429333800750638431302055944420911228116539996595396738593972437975092643832236217609130732045111046071011670854358351134757494506833869137754901540034620623406536339389229266635564512097770619317046934938208445298359949969419275938126799992837644781094265092396383642128522029926994668777315318090424572254871987122722918189768686099562220705623310822485419898057376057202112525778585822541591178208493533109117570357101183004053662032861206103816008760734720125872632310899826241350140400241384154094601482136014989397782164457527429136757014001502339411757178994106215755919853991221744032603130180211557980819892253815932120282995685835996211871344540247504333515420008754206285261941135250646635811748294953004336422748337196799919969345925228918575124551923294804816314322462338342184813999386594221919858307920402382114406396418567034702510708237328779937229644978691588704991703311756953277084678878036723331413991075155954679431597826054343428099259374113441055859597836810264316924719353508828148488534339072835709622829047388865628645344012591725759461849922389249832832147271252272350580867244738618450918640604249740004670690509476074305892875315573416961827795088965035927254095355397325049356712496776445235458945844215038390732185739567757611196823417501793187775961522344073727215583451025896501958150981157762713910044463600564445898448008889518621317037915706548128803420029569755423720409377391389889119671560762202449930841107930541245565936538858110066986105572702598672593834303151332564965310727157270598620259798012668178828096319058442237791422642009618972569571806965609239910882335418194394903837533142071203924631649469503113782630622042180845473651842265678553497575527688847770174589321376165875960870163500526206931628690627664448082688203110995488771583166256113142233868830873513114411473209970565668672292969073739984902139730459625053809890473622057311091258472502116333548076744678487856895200783160920828615668225414057169670147479759699279748066104883711732715954745190252578819389467884937084495611386243652967108695544442500375503530875228294468844574348809005791199893823928131923612501434787472230253645218756920369300264124928029281725508499989433621001314498773171715828288248201856320507671747526931849503521292499580431962795474924755949431850666329499979023879
That gigantic number is the result of multiplying prime numbers together. If you can figure out the prime numbers, you can actually break most bank/corpo grade security. If SIPRNET/NIPRNET (military intranet, existence isn’t classified, shit’s on wikipedia) is still running on shitbox fucking IPSEC tunnels, maybe milspec too. I’m not going to speculate about the computer security of national security assets, though, as there’s being based then there’s being Kevin Mitnick or weev (AKA Andrew Auernheimer, from the Childish Gambino song). Lessons learned.
This is, mathematically, Platonically (in the sense of Forms) speaking, how to securely communicate with another party in an untrusted environment.
These days, the actual math uses something called Elliptic Curves, but that’s beyond the scope of this essay.
PART THREE
So shit hits the fan. You’ve got chickens, your buddy has beans and usually wants some chicken. You have a third friend who has been planing boards. You need lumber, your buddy with lumber doesn’t need chickens or beans. What do you do?
You write him an IOU.
The IOU eventually gets traded to somebody with tomatoes, who needs chickens, and who you don’t need tomatoes from.
Boom, the cycle is closed.
This is the core concept of money, and how it gets reinvented basically every time.
This is not how money currently exists. This is how it starts.
What’s the problem with the IOU system? They’re easy to forge.
If an IOU is hard to forge, then, up until about 2009, it was physical.
This is what has driven the evolution of cash, is forgery. Ask any low effort poster about coin-clipping if you want to learn more.
Be prepared to hear “the fucking jews” about once a minute minimum if you do.
In 2009 Bitcoin hit the world.
Forget everything you know about Bitcoin. Forget about ‘muh power wasted on mining’, all that other shit.
What Bitcoin literally is, is an unforgeable, digital, IOU. You can’t make extra, or more, or inflate it. There are 21 million, the end. You can’t take a Bitcoin from another person without getting their secret numbers. The end. You can do that with a pipe wrench or some clever hacker stuff, but it’s not easy, either way, usually.
Same as cash.
Unlike cash, Bitcoin does not have a central authority. What bitcoin is is millions of people using their computer power to try and find prime numbers. They do this in sequence, stacking primes in such a way that one cannot easily forge the stack. At this time I will not be getting in to the gritty of how that works.
Suffice it to say, if you wanted to forge Bitcoin, you’d need to have AT MINIMUM, more computer power than everyone else mining bitcoin combined, and at this point nation states are mining Bitcoin. The real amount necessary is actually more than this, you’d need to be able to flash-forge the block chain faster than everyone else can mine the next bitcoin block, and those are roughly 10-20 minutes apart these days.
I would say probably a Kardashev 1+ civilization could do this, but almost certainly not any nation or national level actor (think walmart, amazon, etc.) on earth.
The point is, nobody has control over Bitcoin. The people who write the Bitcoin software can release it, but it is up to each individual miner whether or not they use it. At any point, 51% of Bitcoin’s miners could say “My goodness, this situation is most uncouth! We must sally forth to better code versions!” and what they fucked off to or did would be Bitcoin. You can’t print it, you can’t negative-interest-rate it, you can’t confiscate it or freeze it. At any point, any two people using Bitcoin can transact with each other, and you can cope, you can seethe, but unless you can take down the whole net and stop them from meeting each other with laptops or phones, you can’t stop Bitcoin and you can’t take it.
This is why Bitcoin could have unfucked most things.
EPILOGUE
The vast majority of people that talk about this shit do so from either a whitepaper jargon approach (go try to read up on the Internet Computer Project) or they’re selling you something.
It’s important to understand at least on a conceptual level how major things work. Like cars, at this point decentralized currency systems are here to stay.